How To Find The Area Of A Segment Determined By A Major Arc

17 Sep, 2021

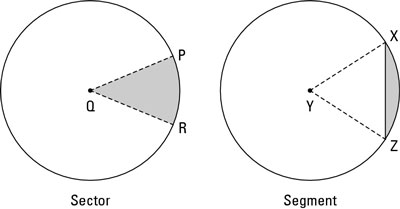
This equations area is derived in the equation Circle -area of sector. Arc A is part of the circle with centre O and radius of PQ.

8th Grade Math Worksheets For Practice I Think My Teacher Should Do This So She Would Know Who Kn 8th Grade Math Worksheets 8th Grade Math Geometry Worksheets

See diagrams below The triangle with angle θ can be bisected giving two right angled triangles with angles θ 2.

How to find the area of a segment determined by a major arc. Multiply this root by the central angle again to get the arc length. The arc length from the familiar geometry of a circle is The area a of the circular segment is equal to the area of the circular sector minus the area of the triangular portion using the double angle formula to get an equation in terms of Θ. To find the segment area you need the area of triangle IDK so you can subtract it from the area of sector IDK.

Sin θ 2 a R. Find the area of the whole sector find the area of the triangle within the sector subtract the area of the triangle from the. The area of the arc segment is defined by the angle θ θ and the circles radius r.

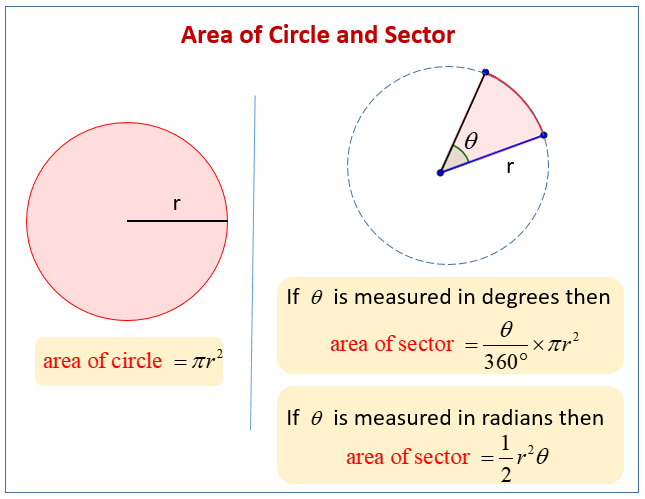
Let r be the radius of the circle. Plug the sectors central angle measurement into the formula. I From the given radius of the circle and measure of the central angle occupied by an arc determine the area of the sector of the circle.

A segment A sector - A isosceles triangle 05 r² α - 05 r² sinα 05 r² α sinα Formula given radius and height. Using this information you. Therefore the measure of 85.

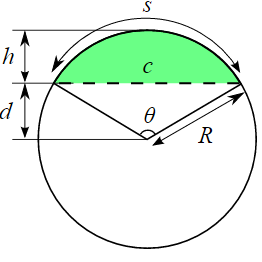
L - arc length h- height c- chord R- radius a- angle. Arc length and area. To calculate the area of a segment we will need to do three things.

Iii Subtract the area of the triangle from the area of the sector to obtain the segment area. Arc Length and Sector Area You can also find the area of a sector from its radius and its arc length. Since a circle has 360 degrees total completing this calculation gives you what portion of the entire circle the sector represents.

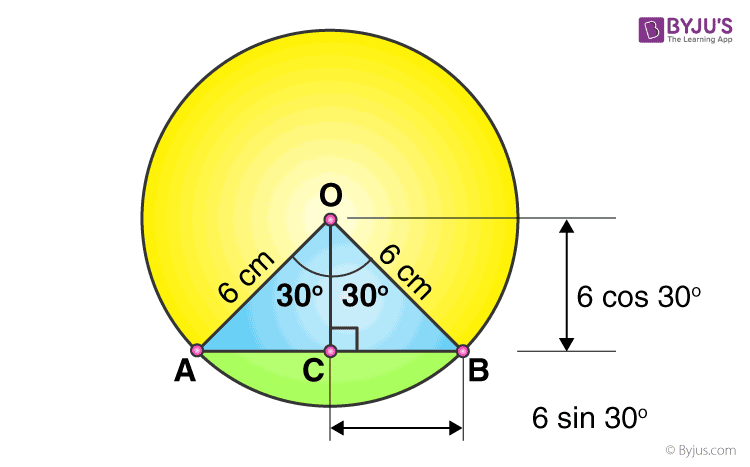
Find the area of circle segment IK. In the circle below there is both a major arc and a minor arc. That creates two 30- 60- 90 triangles.

Look at the circle and try to figure out how you would divide it into a portion that is major and a portion that is minor. Ii Find the area of the triangle formed between two radii and the chord of the segment. For example enter the width and height then press Calculate to get the radius.

Area of the major segment area of the circle area of the minor segment 7065 204 6861 square cm. To calculate the area of a segment bounded by a chord and arc subtended by an angle θ first work out the area of the triangle then subtract this from the area of the sector giving the area of the segment. If you know radius and angle you may use the following formulas to calculate the remaining segment parameters.

Finding the arc width and height. Divide the central angle by 360. Area of the major segment Area of the circle Area of the minor segment 314 10 2 285 cm 2 314 285 cm 2 2855 cm 2 Example 3.

The formula for area of a circle with radius r and arc length. The formula to find the area of the segment is given below. Enter any two values and press Calculate.

The diagram shows two arcs A and B. It can also be found by calculating the area of the whole pie-shaped sector and subtracting the area of. It works for arcs that are up to a semicircle so the height you enter must be less than half the width.

The measure of an arc the measure of its central angle. Doing this will give you what fraction or percent of the entire circle the sector represents. Divide the arcs central angle by 360.

Find the square root of this division. The missing value will be calculated. To find the area of the arc segment we first find the area of the arc sector shown in red in the second image on the right.

Draw an altitude straight down from D to segment IK. You can find the final equation for the segment of a circle area. To calculate arc length without radius you need the central angle and the sector area.

Multiply the area by 2 and divide the result by the central angle in radians. B The area of a segment when the height and length of the chord of the segment are given. A segment r² arccosr-hr - r-h 2 r h - h² where h is the height of a segment also known as sagitta.

If the radius and the segment height of a circle are given then the formula to calculate the area of the segment is Area of Segment r2 cos-1r-hr-r-h2rh -h2.

Lesson Explainer Areas Of Circular Segments Nagwa

Ideas And Resources For The Secondary Math Classroom Sector Area And Arc Length Geometry Interactive Notebook Math Interactive Notebook Teaching Geometry